Nonlinear Models Speed Up Development of Foamed Plastics
Previous Article Next Article
By Abhay Bulsari1 and Markku Talja2
1Nonlinear Solutions Oy, Turku, Finland 2NMC Termonova Oy, Inkoo, Finland
Nonlinear Models Speed Up Development of Foamed Plastics
Previous Article Next Article
By Abhay Bulsari1 and Markku Talja2
1Nonlinear Solutions Oy, Turku, Finland 2NMC Termonova Oy, Inkoo, Finland
Nonlinear Models Speed Up Development of Foamed Plastics
Previous Article Next Article
By Abhay Bulsari1 and Markku Talja2
1Nonlinear Solutions Oy, Turku, Finland 2NMC Termonova Oy, Inkoo, Finland
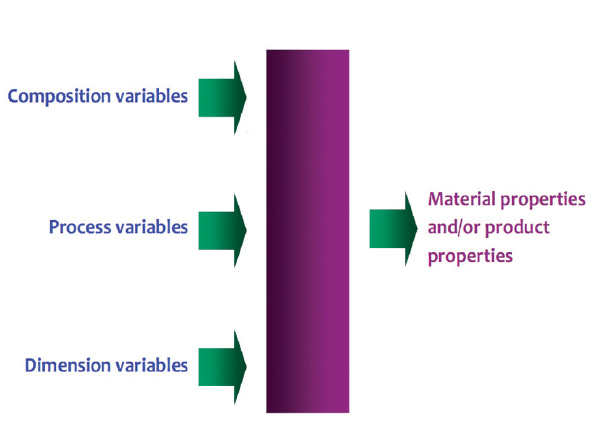
Figure 1: Material properties and product properties depend on composition variables, process variables, and dimension variables.
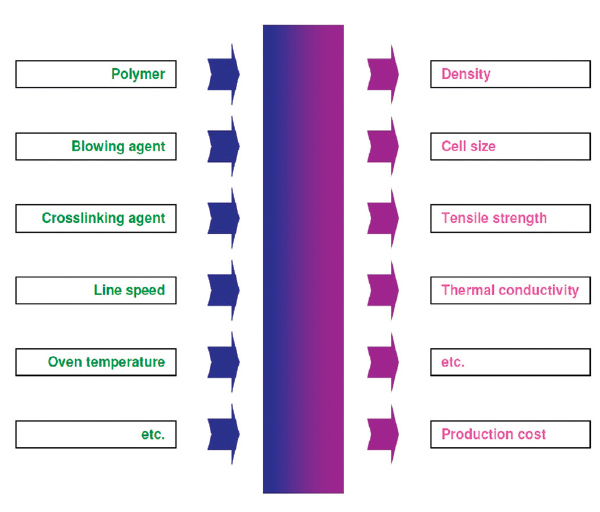
Figure 2: A typical configuration of nonlinear modeling of foamed plastics would have composition variables, process variables, and dimension variables as input variables—and product properties, production rate, raw material cost, production cost, etc. as output variables.
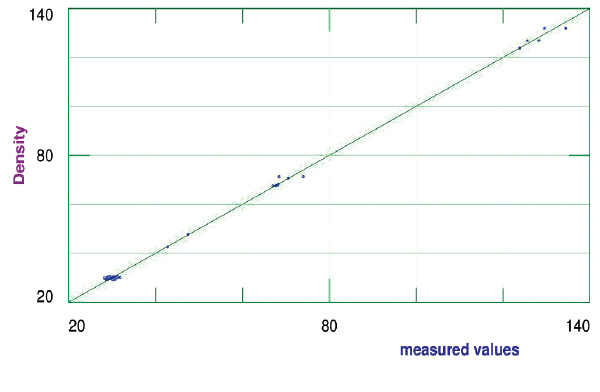
Figure 3: A comparison of the measured values of density with the values predicted by the nonlinear model.
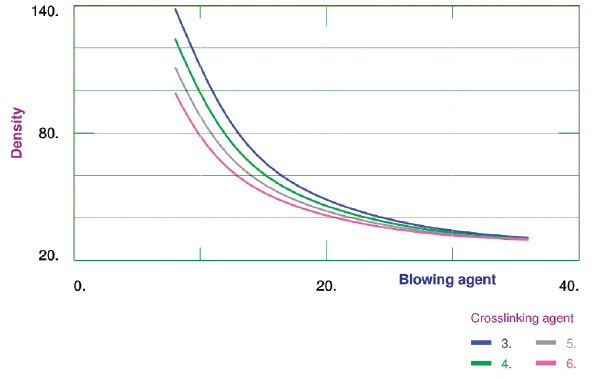
Figure 4: Effect of blowing agent on density with different amounts of crosslinking agent.
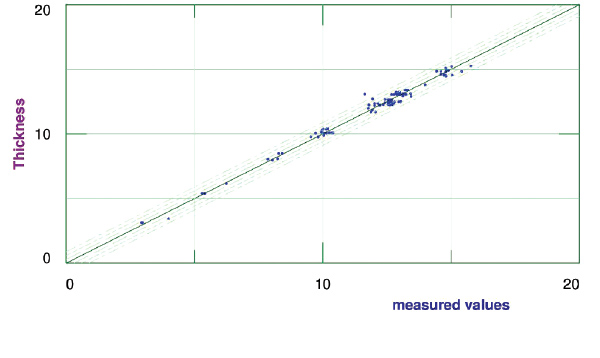
Figure 5: A comparison of the measured values of thickness with the values predicted by the nonlinear model.
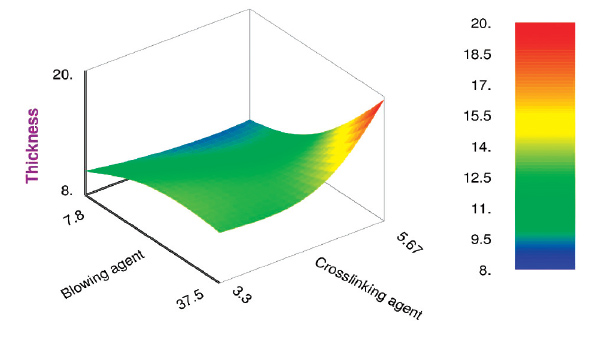
Figure 6: Surface plot of thickness against blowing agent and crosslinking agent.
Product development of various kinds of materials entails achieving desired combinations of product properties from a limited set of raw materials. These product properties usually depend on a large number of variables, including composition variables, process variables, and dimension variables.
The relations between these variables are usually not expected to be very simple or linear. Polymeric materials in particular tend to be more complicated. If the relations between these variables can be described mathematically, we would be able to determine ways of producing the product with desired combinations of properties by working with a set of equations.
Mathematical Modeling
Mathematical modeling can be performed in various ways, and different ways are suitable in different situations. Mathematical models represent knowledge of quantitative effects of relevant variables in a concise and precise form. They can be used instead of experimentation if they are reliable enough. Mathematical models also permit the user to carry out various kinds of calculations, like determining suitable values of variables which will result in desired material properties or product characteristics.
Physical or phenomenological modeling is not particularly effective for predicting material behavior. Physical modeling usually requires assumptions and simplifications. Empirical and semi-empirical modeling, on the other hand, do not need any major assumptions or simplifications. Empirical models simply describe the observed behavior of a system. Empirical modeling is feasible when the relevant variables are measurable.
Conventional techniques of empirical modeling, however, are linear statistical techniques. These tend to have serious limitations because nothing in nature is very linear, and particularly so in materials science. It therefore makes sense to use better techniques of empirical and semi-empirical modeling which take nonlinearities into account.
Nonlinear Modeling
Nonlinear modeling is empirical or semi-empirical modeling which takes at least some nonlinearities into account. Nonlinear modeling can be carried out with a variety of methods. The older techniques include polynomial regression, linear regression with nonlinear terms, and nonlinear regression. These techniques have several disadvantages compared to the new techniques of nonlinear modeling based on free-form nonlinearities.
The newer methods include feed-forward neural networks, series of basis functions, kernel regression, multivariate splines, etc. which do not require a priori knowledge of the nonlinearities in the relations. Among these new techniques, feed-forward neural networks have turned out to be particularly valuable in materials science and process engineering.1
Feed-forward neural networks have several features which make them better tools for nonlinear empirical modeling. Besides their universal approximation capability,2 it is usually possible to produce nonlinear models with some extrapolation capabilities with feed-forward neural networks. The user does not need to know the type and severity of nonlinearities while developing the models.
Neural networks have been in use in process industries for about twenty years.3 The multilayer perceptron, a kind of a feed-forward neural network, is the most common one, on which most neural network applications in industries are based.4-12
Nonlinear Modeling for Materials Development
There is hardly any material behavior which is absolutely linear. Nonlinear modeling has been utilized successfully for various materials including plastics,4-6 rubber,7 metals,8-9 concrete,10 semiconductors,11 mineral wools,12 glass, ceramics, paper, etc. Different materials have different characteristics—different raw materials, different compositions—and are produced by different batch, continuous, or fed-batch processes. However, some things are common to modeling of various kinds of material behavior. Material properties or product properties depend on composition variables, process variables, and dimension variables, as summarized in Figure 1.
For materials development, one would like to determine the best values of composition variables (or feed characteristics), process variables, and/or dimension variables such that the resulting material properties will be within desired limits. The problem looks somewhat similar from the modeling point of view for a wide variety of materials. Nonlinear models make materials and product development more efficient by reducing expensive experimentation and by helping achieve better combinations of material properties, sometimes optimized for cost.
Sometimes the process variables do not matter, or are not independent variables. In some cases, dimension variables like particle sizes may be constant. In such cases, the problem is essentially one of recipe development, in which only composition variables matter and determine material properties.
Nonlinear Modeling of Foamed Plastics
Depending on the application of foamed plastics, certain product properties have specifications. These product properties will depend on the amount of polymer, blowing agent, etc. fed into the process; process variables of extrusion and further processing; and several dimension variables. In case of the Furukawa process in use at NMC Termonova, polyethylene is extruded with a blowing agent and a crosslinking agent as thick sheets or slabs which then pass through an oven where crosslinking takes place, followed by foaming.
Figure 2 shows a typical configuration for nonlinear models of the process. Composition variables include the amount of polymer, blowing agent, and crosslinking agent. Process variables can be variables of extrusion, cooling, and the oven, besides the line speed. Dimension variables can include the width and thickness of the extruded sheet, often called the matrix. Nonlinear models can be developed for product or material properties like thermal conductivity, density, cell size, slab thickness, tensile strength, elongation at break, compression modulus, compression set, and tear strength, and also for production economic variables like production rate, raw material cost per kg of product, production cost, etc.
A good amount of production data was available which had records of the important variables. This article describes some results of the nonlinear modeling only of density and slab thickness.
Modeling of density
Nonlinear models in the form of feed-forward neural networks with sigmoidal activation functions in the hidden layer were attempted in various sizes and configurations with various limitations using the production data of 114 well-selected observations. The nonlinear model for density of the extruded, blown, crosslinked foam had the following statistical characteristics of prediction errors:
Output variable 1: Density
rms err of output variable 1: 0.8950
mean |err| of output variable 1: 0.6995
rms % err of output variable 1: 2.5008
max |err| of output variable 1: 2.8490
Correlation of output variable 1: 0.9984
The results look excellent, considering that the correlation coefficient is 99.84%. The rms error (root mean square error—roughly speaking, the standard deviation of the prediction errors) is 0.8950 kg/m3 and the rms fractional error is about 2.5%. These results can be further improved with better and more data and more input variables, as well as by semi-empirical modeling.
Figure 3 shows a plot of predicted densities from the nonlinear model against measured values. The points lie close to the ideal line, but the deviation from the ideal line can still be reduced in further work.
Figure 4 shows the effect of the amount of blowing agent on density for different amounts of crosslinking agent. As expected, density reduces with increasing amount of blowing agent. Crosslinking agent also produces some amount of gaseous products, which possibly explains why larger amounts of crosslinking agent result in lower densities, and its effect is small when the amount of blowing agent is larger.
Modeling of slab thickness
A good control over the slab thickness is also highly desirable, and becomes easier with nonlinear models. As with density, 114 observations from normal production were available for model development. The nonlinear model for slab thickness of the extruded, blown, crosslinked foam had the following statistical characteristics or prediction errors:
Output variable 2: Slab thickness of the foam
rms err of output variable 2: 0.2975
mean |err| of output variable 2: 0.2268
rms % err of output variable 2: 2.8357
max |err| of output variable 2: 1.4492
Correlation of output variable 2: 0.9852
These results also look very good, considering that the correlation coefficient is 98.52%. The rms error is 0.3 mm, which is small enough, considering that the slab thicknesses are up to around 16 mm. These results can also be improved in the further planned work.
Figure 5 shows a plot of predicted thicknesses from the nonlinear model against measured values.
Figure 6 shows a surface plot of thickness against blowing agent and crosslinking agent. The lowest thicknesses are achieved when the amount of blowing agent is minimal, but a lot of crosslinking agent has been added. The highest thicknesses occur when there is a lot of blowing agent as well as crosslinking agent.
One can similarly see the effects of all the input variables and their cross effects with other input variables. With suitable mathematical tools,4,10 it becomes easy to determine a recipe or process variables for achieving a desired combination of material properties. One can also determine recipes with minimal production cost which also satisfy constraints on product properties and process variables.
Conclusions
Production data often contains valuable information which can be utilized to speed up product development, control the process and improve production economics. Nonlinear modeling is a powerful tool to describe the relations between the composition variables, process variables, and dimension variables with the product properties. New techniques of nonlinear modeling are far more efficient at describing these kinds of relations in plastics/polymer sector industries than are linear statistical techniques which have commonly been used.
The kind of nonlinear models described in this article not only helps speed up recipe development for new products, but allows better control over product properties by tuning the process variables also. Thus, besides the amounts of raw materials, small changes in line speed and oven temperatures can also affect the product properties to small extents, and can thus be used to fine-tune product properties.
References
1. A. Bulsari (ed.), Neural Networks for Chemical Engineers, Elsevier, Amsterdam, 1995.
2. K. Hornik, M. Stinchcombe, and H. White, “Multilayer feedforward networks are universal approximators,” Neural Networks, Vol. 2, (1989) 359-366.
3. A. Bulsari, “Quality of nonlinear modeling in process industries,” Internal Report NLS/1998/2.
4. A. Bulsari, K. Lähteenkorva, E. Suokas, and M. Huttunen, “Models add efficiency to bioabsorbable implant development,” Medical Design Technology, Vol. 19, No. 2 (March 2015) 26-28.
5. A. Bulsari and M. Lahti, “How nonlinear models help improve the production economics of extrusion processes,” British Plastics and Rubber (September 2008) 30-32.
6. A. Bulsari, P. Pitkänen, and B. Malm, “Nonlinear modeling paves the way to bespoke polymers,” British Plastics and Rubber (December 2002) 4-5.
7. A. Bulsari, J. Ilomäki, M. Lahtinen, and R. Perkiö, “Nonlinear modeling speeds up tyre rubber recipe development,” British Plastics and Rubber (June 2015) 28-29.
8. A. Bulsari, I. Vuoristo, and I. Koppinen, “Nonlinear models tune precipitation hardening,” Advanced Materials and Processes,Vol. 168, No. 5 (May 2010) 31-33.
9. A. Bulsari, H. Keife, and J. Geluk, ”Nonlinear models provide better control of annealed brass strip microstructure,” Advanced Materials and Processes (July 2012) 18-20.
10. A. Bulsari, H. Kylmämetsä, and K. Juvas, “Nonlinear models of workability and compressive strength help minimise costs,” Concrete Plant International, No. 6 (December 2009) 36-42.
11. A. Bulsari and V.-M. Airaksinen, “Nonlinear models used to address epi layer uniformity,” Solid State Technology, Vol. 47, No. 7 (July 2004) 33-38.
12. A. Bulsari et al., “Correlation of in vitro and in vivo dissolution behaviour of stone wools using nonlinear modeling techniques,” Journal of the European Ceramic Society, Vol. 27, No. 2-3 (2007) 1837-1841.
Note: Co-author Abhay Bulsari published a related study about bio-absorbable polymers in Medical Plastics News in December 2015 (www.medicalplasticsnews.com/
topics/abhay-bulsari).

